Fractional Polynomials

1. Introduction: "Continuous predictors - to categorize or to model?" (S&R (2010)) - a simple example:

The relationship between between percentage body fat content and body mass index (N=326). For more information see Appendix A 2.1 in our book.

Categorization - how?

3 groups, different cutpoints 5 groups
50 groups  

 

  • Depending on the number and positions of cutpoints, resulting step functions are very different.

  • None of these step functions seem to describe the influence of bmi on percentage body fat well enough

FP model - a better solution

 Data, fit by an FP1 function and residuals

Reproduced from R&S (2008) with permission from John Wiley & Sons Ltd.

  • As shown by the residuals and the related smoother with 95% confidence interval, the FP1 function fits the data well. The pale shaded area shows the inner 95% region of the data.

2. Class of FP functions

The class of fractional polynomial (FP) functions is an extension of power transformations of a variable (Royston & Altman (1994): Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling (with discussion)). For most applications FP1 and FP2 functions are sufficient. General FPm functions are well-defined and straightforward, and occasionally find a use in data analysis and as effective approximations to intractable mathematical functions (Royston & Altman (1997): Approximating statistical functions by using fractional polynomial regression).

 

FP1: β1xp1

FP2: β1xp1 + β2xp2

For the exponents p1 and p2 a set S with 8 values was proposed

S = {-2, -1, -0.5, 0, 0.5, 1, 2, 3}      0 - log x

For p1 = p2 = p ('repeated powers') it is defined

FP2 = β1xp + β2xp log x

This defines 8 FP1 and 36 FP2 models.

The values p1 = 1, p2 = 2 define the quadratic function.

 

The class of FP functions seems to be small, but it includes very different types of shapes.

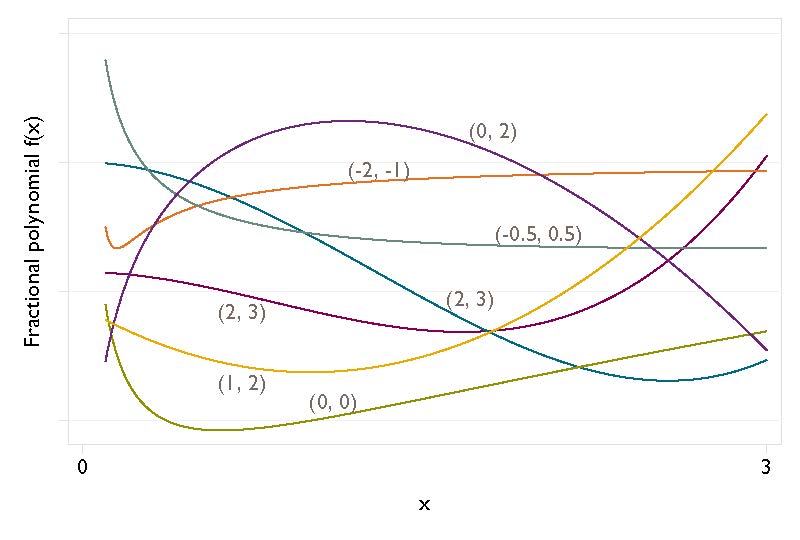
3. How to select a function - FP function selection procedure (FSP)

An FP function should fit the data well, and also be simple, interpretable and transferable.

To assess whether a variable has a significant effect the FSP starts by comparing the best fitting allowed FP (often FP2) function of a continuous variable x with the null model. If significant, the procedure proceeds by comparing FP functions with a ‘simple’ (usually linear) default function. Using FSP the default function is often selected. More complex FP functions are chosen only if they fit the data much better (based on a significance criterion).

Before starting to select a suitable function, the analyst must decide on a nominal p-value (α) and on the degree (m) of the most complex FP model allowed. Typical choices in medicine are α=0.05 and FP2 (m=2). In the following we describe FSP when FP2 is chosen. It is straightforward to adapt the procedure for use with other FP degrees.

Based on the deviance (minus twice the maximized log likelihood)  the best FP1 and best FP2 function are determined. The following test procedure assumes that the null distribution of the difference in deviances between an FPm and an FP(m-1) model is approximately central χ2 on two degrees of freedom. For details see Sect. 4.9.1 of Royston & Sauerbrei (2008).

The FP function is determined for the variable x using the following closed test procedure:

  1. Test the best FP2 model for x at the α significance level against the null model using four d.f. If the test is not significant, stop, concluding that the effect of x is “not significant” at the α level. Otherwise continue.

  2. Test the best FP2 for x against the default (usually a linear function) at the α level using three d.f. If the test is not significant, stop, the final model being the default. Otherwise continue.

  3. Test the best FP2 for x against the best FP1 at the α level using two d.f. FP2 selects two power terms and estimates two corresponding parameters, therefore 4 d.f.; correspondingly FP1 has 2 d.f., giving a difference of two d.f. - If the test is significant, the final model is the best FP2, otherwise the final model is the best FP1. End of procedure.

Reproduced from R&S (2008) with permission from John Wiley & Sons Ltd.

Note that if α = 1 then x is always selected and step 1 is redundant. Using the flavor of a closed test procedure ensures that the overall type 1 error is close to the nominal significance level. For some results concerning type 1 error and power we refer to simulation studies mentioned in 4.10.5 of our book.

4. FPs - key issues and how to try to handle them

4.1 The variable x has to be positive

4.2 Influential points and robustness

Influential points (IPs) and small sample sizes can both have a strong impact on a selected function and on the selected MFP model.
In the univariate context, several issues and ways to handle them are discussed in the book.

R&S (2007): Improving the robustness of fractional polynomial models by preliminary covariate transformation: a pragmatic approach

  • Using the simulated data from the ART study (see Chapter 10), Sauerbrei et al (2023) illustrate approaches which  can help to identify IPs with an influence on function selection and the MFP model.

  • The results showed that one or more IPs can drive the functions and models selected, specifically for smaller sample size. However, when the sample size was relatively large and regression diagnostics were carefully conducted, MFP selected functions or models that were similar to the underlying true model. (see also MFP – 4.4).

4.3 Lack of fit

4.4 FPs are unsuitable for modelling some types of functions

  • If sigmoid curves are relevant, it may be sensible to use the MFPA modification.
    Sigmoid (doubly asymptotic) functions are not represented in the class of standard FP functions. Royston (2014) described an extension of univariate FP modelling via the so-called acd (approximate cumulative distribution) variable transformation which includes a class of sigmoid functions of X. In a further step, Royston and Sauerbrei (2016) proposed the MFPA procedure, which extends MFP by permitting selection of sigmoid functions derived from the acd transformation when supported by sufficiently strong evidence in the data.

  • FPs are global functions and cannot handle local features like splines.
    Binder & Sauerbrei (2010) proposed to systematically check model fits, obtained by the MFP approach, for overlooked local features. Statistically significant local polynomials are then parsimoniously added.
    Binder & Sauerbrei (2010): Adding local components to global functions for continuous covariates in multivariable regression modeling

4.5 Big Data

  • Having a large sample size offers many opportunities for MFP analyses but also raises several issues of our test-based FP function selection procedure. Obviously FSP needs to be adapted because a very large sample size would (nearly) always result in selecting the most complex allowed FPm (typically FP2) function.
    So far we have no experience analyzing ’Big Data’ with MFP or more generally with FP methodology. For thoughts about opportunities and challenges of using MFP in Big Data see Sauerbrei and Royston (2017). We consider two very different 'Big Data' situations: (a) Large(r) sample size (b) Very large number of covariates and relatively small sample size.