The MFP approach combines

  • Selection of variables by using backward elimination (BE) with

  • Selection of fractional polynomial (FP) functions of continuous variables

MFP is a pragmatic procedure to create a multivariable model with the twin aims of selecting important variables and determining a suitable functional form for continuous predictors.

To select a model, significance levels chosen for the two components (BE and FP functions) are the key settings to determine model complexity (more or fewer variables included, simple linear or more complex non-linear functions selected). If an extremely low significance level (e.g. 0.00001) is used to select FP functions, only linear functions are selected and MFP in effect becomes just BE.

Although relatively simple and easily understood by researchers familiar with the basics of regression models, the selected models often extract most of the important information from the data. Models derived are relatively easy to interpret and to report, a pre-requisite for transportability and general use in practice.

Easy to use software is available.

Fractional Polynomials

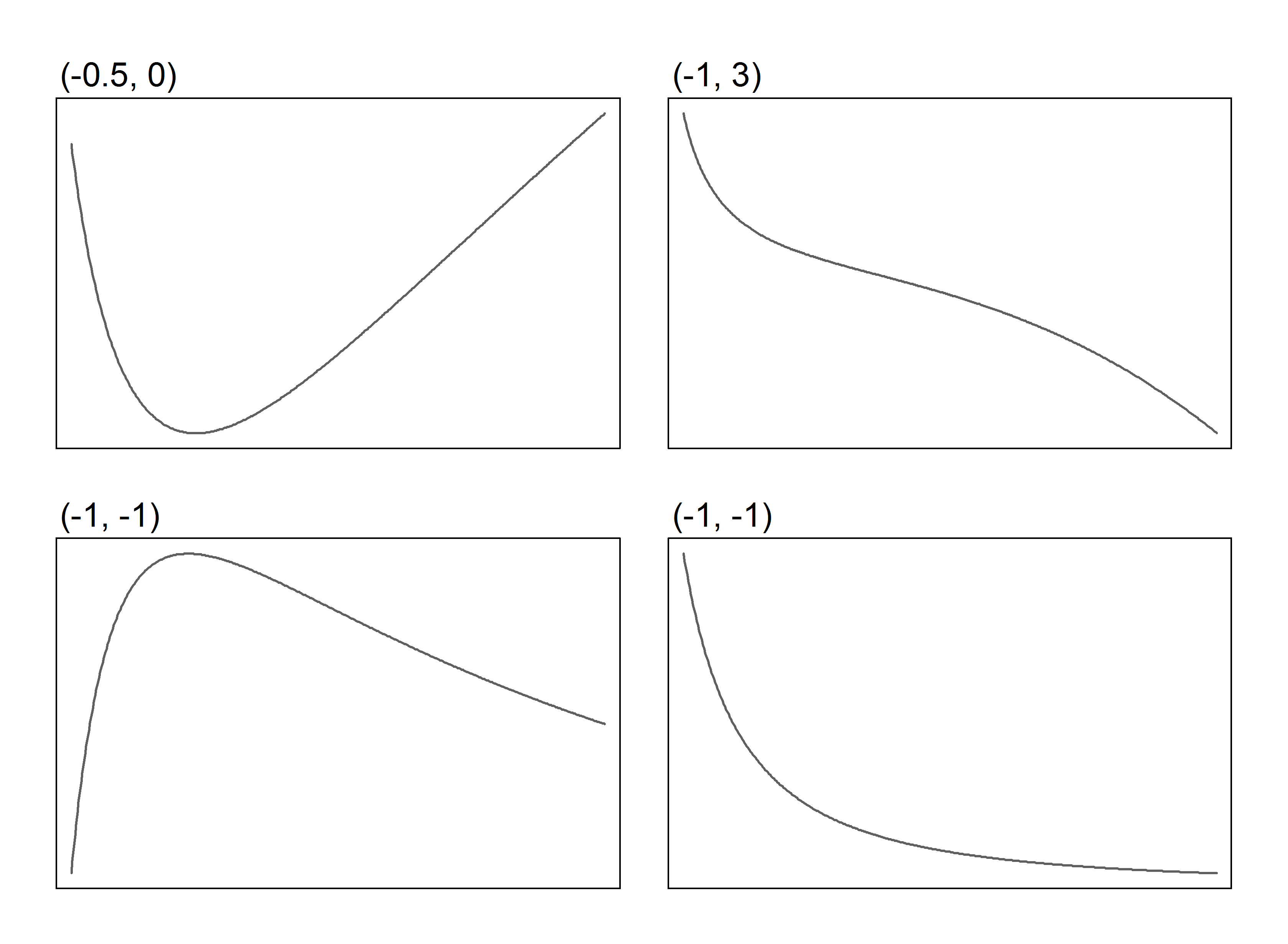
Although simple, the class of FP functions is flexible, for example:


Reproduced from R&S (2008) with permission from John Wiley & Sons Ltd.

 

All four of these functions are second-degree FPs. They have just two regression coefficients and two powers. For example, the top left curve has the following form: β1x-0.5 + β2 log x. The two bottom curves have the form β1x-1 + β2x-1 log x. The bottom two are examples of ‘repeated powers’ FP models.

Developers of MFP and its extensions

image: Douglas Altman and Patrick Royston 1995 at a meeting in Freiburg, Germany

image: Willi Sauerbrei und Patrick Royston 2009

The FP approach, including an early version of MFP, was proposed in 1994 by Patrick Royston and Doug Altman (photo on the left, 1995 at a meeting in Freiburg) and most of the further developments were done by Patrick Royston and Willi Sauerbrei (photo on the right, 2009 at Mathematisches Forschungsinstitut Oberwolfach, Germany).

On this website you will find:

  • Information about key issues of variable selection, function selection and the simultaneous use of BE and FP functions in the MFP procedure

  • Extensions of MFP to investigate continuous variables in different settings

    • For interactions (MFPI; specifically relevant to investigate in randomized controlled trials whether continuous covariates interact with treatment; estimate the treatment effect function)

    • In survival data interactions with time (MFPT; modelling of time-dependent effects)

    • To combine functions in a meta-analysis (METACURVE)

We give only a short introduction to each topic. However, all of the following issues are discussed in detail in our book (links always in red) and/or in related papers (links always in green). We will often refer to our book. You can download datasets and programs on our book website.

 

Royston, P., Sauerbrei, W. (2008): ‘Multivariable  Model-Building – A pragmatic approach to regression analysis based on fractional polynomials for modelling continuous variables’. Wiley.

by naming the number and title of the relevant section(s). Since the book appeared we have extended our work on MFP (for example, comparison of MFP to spline based approaches in a large simulation study) and have transferred MFP methodology for use in meta-analyses. From the huge literature on the topics, we mention only a small number in which none of us is an author or co-author. These papers have had a major influence on our own work.

Under Publications you can find all cited papers categorized by the main topics (FP, Variable Selection, MFP...). Therefore, papers that are relevant to more than one topic may appear in more than one category.